Comment compter les Kongs cachés

Bonjour
J'essaie d'améliorer la page wikipédia relatif aux règles MCR et j'ai un problème sur la façon dont sont comptés les kongs cachés dans les différents combinaisons.
En effet sur le site du MMSP il y a 2 documents à ce sujet
1-Beyond the Green Book-Traduction
2-Combinaisons de kongs

Mais ces 2 documents ne sont pas cohérents
2 ne compte pas la combinaison "2 kongs cachés" pour les combinaisons à 3 et 4 kongs
ainsi la combinaison 1 kong exposé, 2 kongs cachés, 1 pung caché vaut 32+16+6=54 dans le document 2 alors que les 8 points de 2 kongs cachés sont comptés dans 1 pour un total de 62.

Qui a raison ? Je serai tenté de dire 1. 1 parle aussi de 'controversial fan'. Est ce que ça veut dire qu'il n'y a pas d'accord concernant ces combinaisons. Existe il des documents officiels à ce sujet ?

Merci

Liens
1:magicmahjong.fr/index.php?option=com_docman&task=doc_download&gid=231&Itemid=215&lang=fr
2:magicmahjong.fr/index.php?option=com_docman&task=doc_download&gid=250&Itemid=215&lang=fr

ok je vois qu'il y a déjà un topic sur ce sujet
https://mahjong.forum2jeux.com/t693-question-sur-3-kongs

Désolé pour le doublon, mais il semble que les choses ne soient pas très claires

Ma compréhension et qu'on ne compte pas 2 Kongs cachés uniquement pour les cas avec 3 ou 4 kongs cachés.
Du coup le fichier du MMSP est à priori faux car il ne compte que 2 pungs cachés dans les cas avec 2 kongs cachés et 1 exposé.
En plus il y a une coquille, dans le cas 3 kongs, l'astérisque devrait être sur la 2ème ligne et non la 3è

Pas trop de réponses sur ce sujet, je pense qu'on est nombreux à ignorer ce point.
Peut-être que Quentin saura nous éclairer quand il sera de retour de Hongrie.

Salut.

La position officielle, en particulier en France, stipule que l'on ne compte Kong caché (2) ou 2 Kongs cachés (8) que s'il y a respectivement un ou deux Kongs cachés. S'il y a trois ou quatre Kongs cachés, il y a déjà 3 ou 4 Kongs (resp. 32 ou 88 points) et 3 ou 4 Pungs cachés (resp. 16 ou 64 points).
C'est une question très controversée.

Je me suis fait le petit mémo suivant:

Cumul des points pour les Kongs (selon méthode de calcul officielle)
Avec 1 kong :
exposé (1 point)
caché (2 points)

Avec 2 kongs :
2 exposés (4 points)
1 exposé + 1 caché (6 points)
2 cachés (8 points)

Avec 3 kongs :
On compte 32 points de toute façon
avec 1 kong caché + 0 point (pour 1 pung caché)
avec 2 kong cachés + 2 points pour "2 pungs cachés"
avec 3 kongs cachés + 16 points pour "3 pungs cachés"

Avec 4 kongs :
On compte 88 points de toute façon
avec 1 kong caché + 0 point (pour 1 pung caché)
avec 2 kongs cachés + 2 points pour "2 pungs cachés"
avec 3 kongs cachés + 16 points pour "3 pungs cachés"
avec 4 kongs cachés + 64 points pour "4 pungs cachés"

J'avoue m'être pas mal torturé le cerveau sur la question. On voit d'ailleurs que dans le lien sur un topic "Kong" que j'avais lancé en 2011, y a eu beaucoup de réponses et pas toujours dans le bon sens.

Heureusement, 3 kongs dans une main, c'est rare !!!

A+ et bon jeu

Eek

J'avoue que je ne saisis pas trop quelle est la logique. Car du coup,
1KE + 1KC + 1KC + 1 PE rapporte la même chose que 1KE + 1KE + 1KC + 1 PC
Alors qu'il est plus facile de faire des Kongs exposés que cachés. C'est d'ailleurs admis dans le cas de 2 kongs.

J'avoue également ne pas vraiment bien comprendre toute la logique du calcul sur une main à 3 kongs. Après plusieurs recherches, j'en suis arrivé à cela. Un petit exemple pour être clair.

Supposons la main suivante:

- - - -


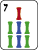
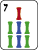
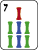
4444 Bambou/3333 Caractère/6666 Caractère/777 Bambou

Exposé-Exposé-Exposé-Exposé___Trois kongs (32) + Tout pung (6) + Tout ordinaire (2) + Finir sur paire (1) soit 41 pts.
Exposé-Exposé-Exposé-Caché____Trois kongs (32) + Tout pung (6) + Tout ordinaire (2) soit 40 pts.
Caché-Exposé-Exposé-Exposé____Trois kongs (32) + Tout pung (6) + Tout ordinaire (2) soit 40 pts.
Caché-Exposé-Exposé-Caché_____Trois kongs (32) + Tout pung (6) + Tout ordinaire (2) + Deux pungs cachés (2) soit 42 pts.
Caché-Caché-Exposé-Exposé_____Trois kongs (32) + Tout pung (6) + Deux pungs cachés (2) + Tout ordinaire (2) soit 42 pts.
Caché-Caché-Exposé-Caché______Trois kongs (32) + Tout pung (6) + Trois pungs cachés (16) + Tout ordinaire (2) soit 56 pts.
Caché-Caché-Caché-Exposé______Trois kongs (32) + Tout pung (6) + Trois pungs cachés (16) + Tout ordinaire (2) soit 56 pts.
Caché-Caché-Caché-Caché_______Trois kongs (32) + Quatre pungs cachés (64) + Tout ordinaire (2) soit 98 pts.

On voit bien qu'il n'y a pas de récompenses sur un kong caché par rapport à un simple pung caché. J'avoue que la logique pour moi n'y est pas. Je m'explique:

caché - caché
Etape 1 : on compte le kong, soit 8 points pour 2KC
Etape 2 : on transforme le kong en pung et on calcule. Ici 2 pts pour pung de dragon + 2 pungs cachés (0pt car inclus dans 2KC)

En suivant la même logique, sur mon exemple un peu plus haut sur la ligne KC KE KE PC, je calculerai personnellement:
Etape 1 :Je regarde les kongs globalement 3 kongs 32 pts
Etape 2 : Je regarde les cachés => 1 KC +2pt
Etape 3 : je transforme les kongs en pung et je regarde globalement => Tout pung 6pts
Etape 4 : je regarde les cachés => 2 pungs cachés +2pts
Etape 5 : les points annexes : Tout ordinaire +2pts

Total : 44 pts. Mais ici on ne peut en compter que 42 car l'étape 2 est apparemment non conforme.

Alors, qui pourrait encore donner son avis sur la question pour qu'on y voit clair?

Le doc "beyond the green book" est quasi parfait à mon sens pour le comptage des points sur les kong, sauf sur un domaine.

Dans les cas de 3 et 4 kongs et que l'on a 2 kongs cachés, selon moi on ne doit pas compter les 8 points de 2 kongs cachés mais seulement 4 points (2*2 pour 2* 1 kong caché).

En effet, si l'on décompose le fan 2 kong caché on a : 4 pts pour 2 kongs + 2pts pour le 1er kong caché + 2pts pour le second kong caché, ce qui fait le total de 8 pts.

Donc, dans cette logique, puisque les kongs sont déjà comptabilisés dans les fan 3 ou 4 kong, on ne doit rajouter uniquement les 2pts de ceux qui sont cachés.

Et tout ceci indépendamment de la présence de X pung cachés.

donc dans un exemple:



cas 4KC :
4K (88) + 4PC (64) + 4*1KC (4*2)

cas 2KC + 1KE +1PE :
3K (32) + 2*1KC (2*2) + TP (6) + 2PC(2)

Il faut toujours se poser la question de : "que peux on avoir ensemble ou pas". C'est le même raisonnement de calcul que pour des mais type 4 chow purs superposés ou main verte.

Dans cette dernière, on compte soit semi pure, soit main pure suivant le cas de figure, bien que si c'est pas l'un c'est forcément l'autre. Idem sur le 4CPS, on a forcément une famille absente, pourtant on peut la compter car on peut être aussi en semi pure ou en main pure...

Donc sur le dernier exemple, je compte les 2 KC (séparément) et aussi les 2PC car je peux avoir 2PC sans avoir de kong, comme je peux avoir un KC sans avoir 2PC... En revanche, je ne compte pas les 8 pts de la fan 2KC car les kongs sont déjà comptés dans la fan 3 kongs. Je n'ajoute que 2es 2 pts de KC (2 fois) car je peux avoir 3 kongs sans kongs cachés...

Explication peut être brouillon.... certainement sujette a controverse...

pazair a écrit:

Le doc "beyond the green book" est quasi parfait à mon sens pour le comptage des points sur les kong, sauf sur un domaine.

Dans les cas de 3 et 4 kongs et que l'on a 2 kongs cachés, selon moi on ne doit pas compter les 8 points de 2 kongs cachés mais seulement 4 points (2*2 pour 2* 1 kong caché).

En effet, si l'on décompose le fan 2 kong caché on a : 4 pts pour 2 kongs + 2pts pour le 1er kong caché + 2pts pour le second kong caché, ce qui fait le total de 8 pts.

Explication peut être brouillon.... certainement sujette a controverse...

La controverse est généralisée, mais ton principe est très intéressant et je pense qu'il sera proposé à Chongqing.

D'après mes souvenirs, on ne compte les kongs cachés que si on a au plus 2 kongs cachés. Mais là-dessus tous les arbitres ne sont pas d'accord. Certains disent que les kongs cachés ne peuvent être comptés que s'il y a au plus 2 kongs...

Pour moi, il faut supprimer l'élément de marque Deux Kongs cachés (8). Il cause deux aberrations.
La première aberration qu'il cause survient lorsque la main contient deux kongs cachés sans pung caché supplémentaire. L'implication Deux Kongs cachés => Deux Pungs cachés fait qu'on ne compte que 8 points, alors que 10 pourraient être comptés avec :

• Deux kongs (4) ;
  
• 2*Kong caché (2*2) ;
  
• Deux Pungs cachés (2).
  

Ce genre de comptage est interdit pour l'instant, à tel point que l'on parle, non sans ambiguïté, de Deux Kongs exposés (4)...

Or ce point particulier est en contradiction avec (ou une exception à) un des cinq principes de comptage, qui est que le gagnant est libre de choisir quel ensemble d'éléments de marque il décide d'appliquer à sa main, quand il peut choisir parmi plusieurs, par exemple :
, gagné sur ,
peut faire l'objet d'au moins trois comptages :

• Sept paires pures consécutives (88), Tout ordinaire (2), soit 90 points ;
  
• Sept paires (24), Main pure (24), Tout ordinaire (2), soit 50 points ;
  
• Main pure (24), Tout caché (2), Tout Chow (2), Tout ordinaire (2), soit 30 points...
  

Libre au gagnant de choisir ce qu'il décide de marquer, et aucun adversaire ne peut lui forcer de compter plus ou moins...


La seconde aberration survient lorsqu'il y a au moins 3 kongs, mais arrêtons de tartiner là-dessus car il va y avoir des petits réajustements sur certains points de règle à l'occasion du championnat du monde.

pazair a écrit:

donc dans un exemple:



cas 2KC + 1KE +1PE :
3K (32) + 2*1KC (2*2) + TP (6) + 2PC(2)

Ton explication est très claire et je suis tout à fait d'accord avec toi sur la méthodo:
Etape 1 : tu comptes les points pour les kongs
Etape 2 : Tu ajoutes des bonus s'ils sont cachés (normal, c'est plus dur en caché qu'en exposé)
Etape 3 : Tu transformes les kongs en pung et on continue les calculs (ici Tout pung et 2 PC)

Le seul "HIC" aujourd'hui, c'est qu'à partir de 3 kongs, l'étape 2 ne doit officiellement pas se faire ... "Beyond the Green Book" n'est pas un réglement officiel (bien que ce soit un très beau document très explicatif). Et si un jour on peut les compter, faudra tomber d'accord sur "combien".
Si on reprend ton exemple, le "bonus" des 2 KC, aujourd'hui on compte 0. Demain, on fait quoi: 8 ou 4 ?

Baaaaaah c'est compliqué. Heureusement qu'on n'en fait pas tous les jours des kongs !!!

A+